2) 0-1 Knapsack Problem

0-1 Knapsack Problem

 

 

Fractional Knapsack Problem

- Greedy 

 

0-1 Knapsack Problem

- Dynamic 

- Backtracking

- Branch and Bound

 

0-1 Knapsack Problem

0-1 knapsack 문제는 greedy 방식으로 optimal을 보장할 수 없다.

0-1 knapsack 문제의 optimal을 보장하기 위해서는 dynamic, backtracking, branch and bound 3가지 방식을 이용해야 한다.

 

 

1) Dynamic

동적 알고리즘은 먼저 입력 크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해경하여, 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘이다.

 

- bottom - up 방식이다

- 노드 간의 관계, 부분 문제들 사이의 관계가 서로 의존적이다.

- 큰 문제의 최적 해에 작은 문제의 최적 해가 포함된다.

- 즉, principle of optimality 최적성 원칙을 가지고 있어야 한다.

 

 

2) Backtracking

백트랙킹 기법은 해를 찾는 도중에 '막히면' (즉, 해가 아니면) 되돌아가서 다시 해를 찾아가는 알고리즘이다.

 

- DFS 방식으로 탐색

- 최적화 문제와 결정문제를 해결할 수 있다.

- state space tree를 구축해 문제를 해결한다.

 

 

3) Branch and Bound

각 노드를 검색할 때마다, 그 노드가 promising 한 지의 여부를 결정하기 위해서 한계값(bound)을 계산한다.

만약 그 bound가 지금까지 찾은 최적의 해답보다 좋지 않은 경우에는 더 이상 가지를 뻗어서 검색할 필요가 없다.

이 경우 가지는 non-promising 하다고 할 수 있다.

 

- Best-First Search

bound : 노드로부터 가지를 뻗어나가 branch를 얻을 수 있는 해답지의 한계

* 주의 * backtracking에서는 bound값이 필요 없다.

 

 

Dynamic 0-1 knapsack

i > 0이고, w > 0일 때,

전체 무게가 w가 넘지 않도록 i번째까지의 항목 중에서 얻어진 최고의 이익(optimal profit)을 P [i][w]이라고 하자.

if wi ≤ W, P[i][w] = maximum (P[i-1][w], pi + P[i-1][w-wi]) if wi > W, P[i][w] = P[i-1][w]

 

P [i-1][w] : i 번째 항목을 포함시키지 않는 경우 최고 이익

pi + P [i-1][w-wi] : i 번째 항목을 포함시키는 경우 최고 이익

 

W는 상수인데 상수값에 시간복잡도가 영향을 받는다.

O(min(2^n, Wn))

 

Backtracking 0-1 knapsack

DFS로 찾아 안 되는 경우에 backtracking 하기

 

 

 

Branch and Bound 0-1 knapsack

bound = (profit + 넘치기 전까지의 이윤의 합) + (W - totalweight) / wk(k번째무게)*pk(k번째이윤)

if(bound(v) > maxprofit)    for (each child u of v){       if(profit(u) > maxprofit)           maxprofit = profit(u);       if(bound(u)) > maxprofit)           insert(PQ,u);}

 

branch and bound 기법으로 최적해를 구하시오.

bound값보다 더 좋은 값이 나올 수 없다.

maxprofit 값은 실제 profit 값을 업데이트한다.

 

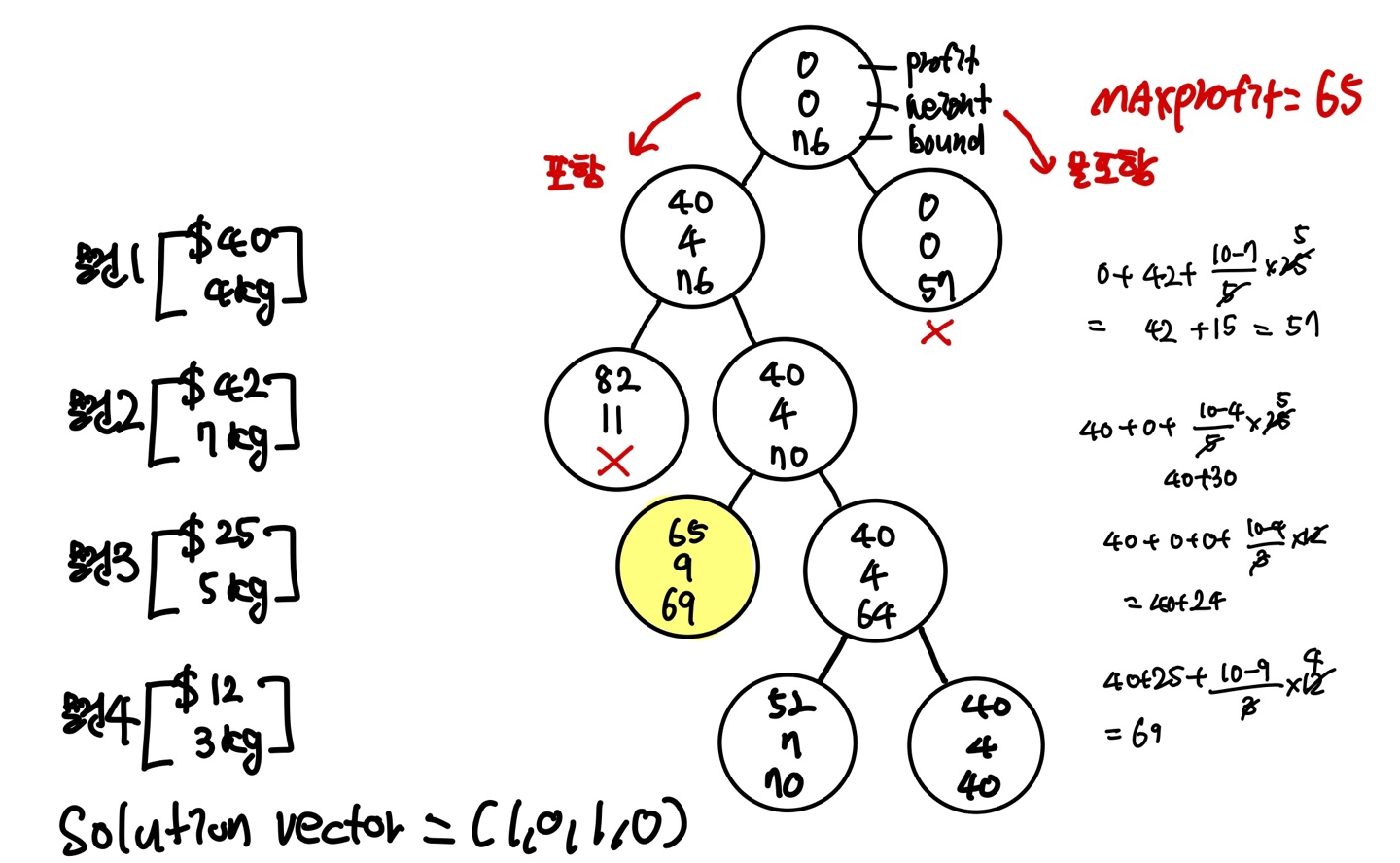
점검 노드의 수  : O(2^n)